Why is Local Volatility Model inappropriate for Cliquet trades
Local volatility model generates the forward (skews estimated for a future date) skews that are too flat. Stochastic volatility models or the Jump diffusion models on the other hand estimate forward skews that have shapes similar to that observed in the market today. This significant consequence is not obvious and can be worked out only when studying/researching the model in detail. This consequence has a significant impact when pricing the forward skew dependant trades such as Cliquets. Many market players have lost a lot of money due to lack of knowledge of this property.
Let's assume we have a locally capped, globally floored cliquet based on periodic contribution to the final coupon.
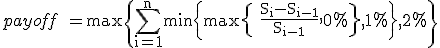
The final payoff is a sum of periodic contributions (say monthly) with each contribution capped at 1% and floored at 0% and the sum of all contributions is subject to the global floor of 2%. If we ignore the global floor, the payoff could also be viewed as comprising of periodic payments subject to a floor of 0% and cap of 1%. Essentially then, we have a series of forward starting call spreads.
A call spread is a skew sensitive strategy. Suppose we are long a call option with strike k1 and short a call option strike k2>k1, the value of the call spread increases with the skew. (Remember option prices increase with increasing implied vol). With increasing difference in implied volatilities 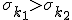 the value of the call spread also increases.
the value of the call spread also increases.
It thus becomes clear that the local volatilty would underestimate the price of this cliquet payoff and indeed the numerical experiments confirm that stochastic volatility models as opposed to the local volatility model generates higher (and more accurate) prices for cliquets.









