Risk analysis of Autocallable notes
Autocallables are quite commonly traded exotics with quite a few variations in structures. As the names suggests, these structures get automatically redeemed (or autocalled) when the the underlying price breaches the autocall barrier. Essentially the maturity of the trade is not fixed, the trade might autocall on any of the observation dates prior to final observation (or expiry) date. Lets begin with the simplest autocall structure and later on we shall discuss some more complicated variations.
Single Asset Autocalls
Lets say we have a 4 year trade with annual observations. The buyer receives coupon say 15% of the Notional Amount on each payment date (a week after the observation date) given that the underlying stock is above 70% of the stock price at inception (Barrier B) and trade has not be autocalled yet. The trade gets autocalled on any of the observation date if it the underlying asset price is greater than the Autocall trigger level (Barrier H=110%).
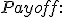
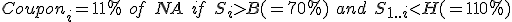
figure 1-Stock price as a percentage of price at inception
| Year 1 | Year 2 | Year 3 | Year 4 | |
|---|---|---|---|---|
| Scenario 1 | 98% | 80% | 101% | 104% |
| Scenario 2 | 88% | 92% | 130% | 105% |
| Scenario 3 | 106% | 98% | 67% | 76% |
Lets take the first scenario. The stock is above the coupon barrier (=70%) at the end of each year and at the same time it never breaches the autocall barrier(=110%). As a result the note pays a coupon of 11% for each of the 4 years. The buyer gets back the notional at the end of the fourth year.
In the second scenario, the stock breaches the autocall barrier in the third year. Consequently, the trade expires in the third year. Because the stock price is above the coupon barrier for each of the three years the trade is live, the note pays a coupon of 11% for the first three years. The buyer gets back the notional at the end of the third year.
Similarly for the third scenario, the note pays a coupon of 11% at the end the first, second and the fourth year. The buyer gets back the notional at the end of the fourth year.
Investment motivation
An autocallable is a yield enhancing strategy. The investor receives an above market yield and in turn he risks not receiving any coupon if the stock is stock is below the coupon barrier (70% in the example above) on the observation date. If the stock however breaches the autocall trigger(110%) trigger, the trade expires and the investor gets back the investment. This would be the case when the market rallies, the investor would be happy to get his investment back which could be deployed in a more bullish strategy (or simply in equity).
Risk Analysis
To understand the risk factors of an autocallable note it helps if we visualize the autocallable payoff as a series of digital payouts with each payout being contingent on the stock being above the coupon barrier on the given observation date but not being above the autocall barrier on any of the previous observation dates. The risks of an autocallable would hence be quite similar in nature to the risks of a digital option.
The buyer of the autocallable note would be long the forward (meaning long the underlier, short the dividends and long the interest rates). He would also be long the skew (think of digital payouts as spreads).
Equity/Interest rate correlation (EQ/IR)
Autocallable is a structure in which the Interest rate/Equity correlation plays an important role. This is because the expiry of the autocallable is not fixed and depends on the performance of the equity. To make things clearer lets assume we have a 5 year autocallable structure that has an autocall trigger at 110% of the initial stock price. For simplicity we assume that the structure just has one autocall observation say 2 year after inception i.e if the stock price is above 110% of the inital level after 2 years, the trade expires otherwise the trade continues till 5 years. We assume that the structure is already delta hedged and the seller buys 2year and 5year zero coupon bonds to hedge his interest rate exposure. (Ahhh!!! Now do you start seeing why the stopping time expiry makes a difference.)
Lets first say the EQ/IR correlation is positive. So if the equity increases, there is a higher probability that the structure will be autocalled after 2 years. The seller sells some of 5 year zero coupon bonds he holds and buys some more 2 year zero bonds. Also since EQ/IR correlation is positive, the interest rates would on average have increased. He would incur a net loss on selling 5 year zero bonds and buying 2 zero year bonds as the interest rates increased and hence price of the bonds decreased meaning that he sells the 5 year bond at a loss and the 2 year bond would be still cheaper to buy. The impact would however be higher for a larger maturity (compounding). So the seller incurs a loss when equity rises and EQ/IR is positive. Now if the equity falls (meaning the interest rates also fall), the probability of the structure being autocalled decreases. So to hedge his exposure the seller sells some of his 2 year bonds and buys 5 year zero coupon bonds. Since the interest rates have also fallen, the bonds would have become more expensive. He makes some profit by selling 2 year bonds but he makes a net loss as the 5 year bonds would have become even more expensive. Again the seller incurs a loss while hedging.
Lets assume now that the EQ/IR correlation is negative. So if the equity increases, the interest rates would fall on average so that the bond prices would increase. Increase in equity increases the probability of the structure being autocalled at the 2 year mark. To hedge the seller would sell some 5 year bonds and but 2 year ones. Since he makes more profit by selling 5 year bonds than he loses on buying 2 year bonds, the seller makes a net profit when equity increases and EQ/IR correlation is negative. It can be argued in similar fashion (and is left to the readers to do that the seller makes a net profit again when the equity falls.
So to summarize when the EQ/IR correlation is positive, the seller makes losses while hedging the interest rate exposure and when the EQ/IR correlation is negative, the seller makes a profit while hedging the interest rate exposure. This loss/profit should be compensated while pricing the structure. So pricing models that assume deterministic interest rates(or EQ/IR correlation=0) would underprice the structure when EQ/IR correlation is positive and overprice when EQ/IR correlation is negative.
Single asset autocallables with down and in Put feature
If the investor thinks that the stock would never fall below a certain level during the life of the trade, he could could work up the coupon for the autocallable by adding a short down and in put feature to the structure. So in the resulting payoff, the buyer receives the autocall coupon whenever the stock is above the coupon barrier and the trade has not been autocalled. In the final settlement either on the contractual maturity or when the trade gets autocalled, the buyer gets back the notional if the coupon barrier is never breached otherwise the actual return on the underlying stock if the coupon barrier is indeed breached on any of the previous observation dates.
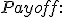
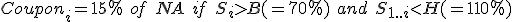
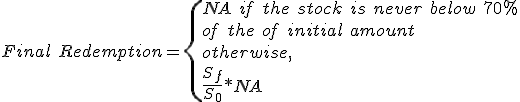
Snowballing Coupon
This feature is seen mostly when the autocall trigger level is equal to the coupon trigger level. It means that whenever the trade pays coupon it gets autocalled too. If the trade is still alive after i observations, the investor sometimes receives the sum of all previously missed coupon (and hence snowball coupon).
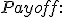
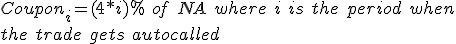
MultiAsset worst-of Autocallables
In the worst-of autocallable trades the buyer receives the coupon C whenever none of the underliers (this a basket trade), is below the coupon barrier level. The trade pays back the notional when the trade expires i.e the autocall date if the trade is autocalled otherwise the contractual maturity.
In a variation of the above structure, the buyer could be short down and in worst of put. This feature is generally added to increase the coupon at the risk of not receiving a portion (or even the entire notional) of the notional amount.









