Risk analysis of Cliquets
Cliquets are one of the most popular structures traded. These are also known as ratchet options due the resetting strikes in the structure. This resetting strike feature is what makes cliquet structures unique as they create an exposure on the forwad skew and vega convexity (we'll come back to this). First lets look at the payoffs of the two commonly traded cliquet structures.
Payoffs
Among the cliquets, the two most commonly traded variations are the Global Cap Local Floor (GCLF) and the Local Cap Global Floor (LCGF). Their payoffs are given below:
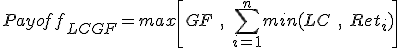
where GC is the global cap and LF is the local floor prestated in the trade terms. Obviously, n*LF should be less than the GC for the payoff to make sense.
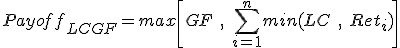
where GF is the global floor and LC is the local cap stated in the trade terms. Again, the GF should be less than n*LC.
Trade motivation
Cliquets could be viewed as a series of forward starting options. This strategy locks in periodic returns from the underlier unlike the conventional european options.Lets suppose we have a local floor global cap cliquet option and further the local floor is 0 and the global cap is set as 18%. Figure 1 below shows the sample payoffs of this structure under three scenarios and compares it with the payoff of a standard european call. The returns shown in the figure are periodic say yearly.
figure 1-Payoffs for a cliquet option
| Year 1 | Year 2 | Year 3 | Year 4 | GCLF | European call | |
|---|---|---|---|---|---|---|
| Scenario 1 | 2% | 5% | 6% | 2% | 15% | 15.797% |
| Scenario 2 | -30% | 2% | 5% | 6% | 13% | 0% |
| Scenario 3 | 2% | -5% | 6% | -3% | 8% | 0% |
In the first scenario in which the stock always increases (example-in bullish market where the stock rallies), the normal european call outperforms the cliquet payout. In the second and the third scenario, (example-an extremely volatile market especially after a crash or indeed as the second scenario indicates a sort of crash in the first year followed subsequent steady recovery) the cliquet outperforms the standard call option.
Because the structure locks in periodic returns which are subject to a floor of 0, the trade picks up only positive periodic performances which could be a strategy employed in volatile markets. Also the investor benefits when the future volatility of the underlier increases. After all, he's been charged for a specific implied volatility, if the realized volatility is infact greated than the expected, he benefits from a wilder positive underlier moves.
Risk analysis
First lets look at the global cap local floor cliquets. If we breakdown the payoff:
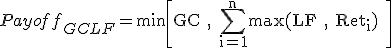
which can be rewritten as
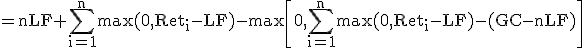
The payoff has been simply broken into three components, first the fixed component = n time the local floor, the second is the excess return of the asset over the local floor - simply put its a series of forward starting call option with strike LF, the third component is the subtracts the excess return over the global cap - which can be viewed as a compound option with strike GC-nLF (remember GC-nLF will be greater than zero for the cliquet payoff to make sense)
First lets talk about the vega, both the forward starting options(second component) and the compound option (the third component in the expression above) increase in value with increase in volatility. However since the buyer is actually short the compound option and long the series of forward starting options, the net vega whether positive or negative would be determined by the values of Local Floor and the Global Cap. For example, if the Local Floor is zero, the buyer is long a series of ATM forward starting options and as we know that the vega for ATM options are the maximum, the first component in the above expression might dominate and the buyer might actually be long vega.
We know that ITM call option benefits from skew, whereas an OTM call option is short the skew. The second component max(0,Reti-LF) whether long or short the skew, depends on the value of LF. If LF
>0, the option becomes OTM whereas when LF<0, the option becomes ITM. The position in the third component (the compound option) is not clear. Likewise, the overall skew position in cliquets is not clear.
Compound options generally have high exposure to vega convexity (dvega/dvol). Hence the overall structure becomes sensitive to the vega convexity.
Now we consider, Local cap global Floor cliquets.
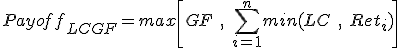
We know caps can be viewed as a combination of long asset and short OTM call options and as we do know that OTM call options are short skew [OTM puts and ITM calls are costlier in the presence of a skew] making the cap structures for the buyer long skew. As a result the LCGF cliquet structure, is long skew for the buyer.
Depending on whether what the values of the local cap and global floor are, the LCGF cliquet structure has exposure to vega convexity. [Remember ATM options calls & put have lower vega convexity (dvega/dvol)].
Related Articles
- Volatility - Sticky strike vs Sticky delta
- Risk analysis of Lookback options
- An introduction to the gamma risk
- Introduction to Martingales and Markov processes
- Introduction to risks in CPPI products









