Revision sheet for Equity Derivatives
The Forward Price
The forward price F=Se(r-q)t, where S = stock price; r = continuosly compounded interest rate; q = continuos dividend rate ; t = time to expiration.
Black Scholes Option Pricing Formula
European Call Price C = Se-qtN(d1) - Ke-rtN(d2)
European Put Price P = -Se-qtN(-d1) + Ke-rtN(-d2) where
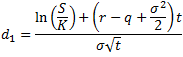
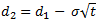
S = Spot price; K = Strike price; t = time to expiry; q = continuos dividend yield; r = risk free interest rate; σ = annual return volatility
Put-Call Parity
Put price + Spot price (minus PV of future dividends) = Call price + PV of Strike price
P + Se-qt = C + Ke-rt
Volatility Skew
In Black Scholes, implied volatility is assumed to be the same for all strikes for a given security. In reality however, for a given time to maturity, implied volatility is generally higher for lower strike prices and lower for higher strike prices.
Volatility Term Structure
Implied volatility varies as a function of time-to-maturity. Typically implied volatility is found to be mean reverting - Short dated implied volatility is more variable than long dated implied volatility.
- During crisis: short dated volatility >> long dated volatility
- In quiet times: short date volatility < long date volatility
Calendar Spreads
Long a Calendar spread: Buy long dated and sell short dated options (same strike and underlying). Investor in a Long calendar spreads expects long dated option price to increase more than the short dated option price. In other words they expect long dated volatility to increase more than short dated volatility.
Short a Calendar spread: Sell long dated and buy short dated options (same strike and underlying).
The Greeks
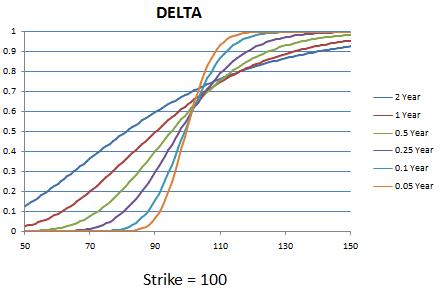
Delta: Rate of change of option price with respect to the underlying stock. Delta for a call = e-qtN(d1) ; put = -e-qtN(-d1)
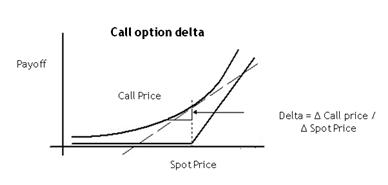
The option delta vs Spot price graph for a European call and put has plotted below.
Variation in delta vs Spot profile for a call option with time to maturity is plotted below: (K = 100).
Gamma: Rate of change of option delta with respect to the underlying stock price. Gamma for a call
(and put) = 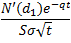
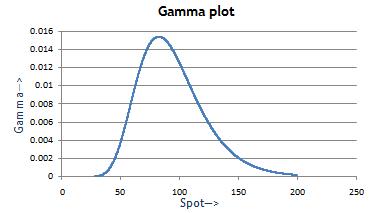
Below is plot of option gamma variation with Spot price.
Variation in gamma vs spot profile with time to maturity is as follows:
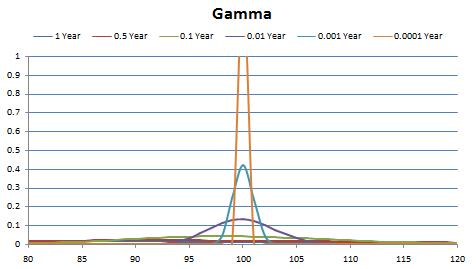
Unlike delta which is bounded between 0 and 1 for a call option and -1 and 0 for a put option, Gamma for a long position in an option can assume any value from 0 to infinity. Gamma is maximum for ATM optiona at expiry.
Vega: Rate of change of option price with respect to underlying stock volatility. Vega for an option (call and put) =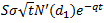
The vega plot plot for European call and put is given below.
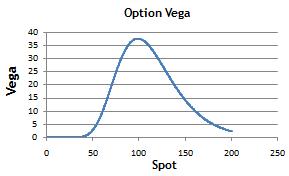
Theta: Sensitivety of option price with respect to time to expiry.
Option Traders Jargon
Selling/Buying gamma: selling/buying short-dated options. (Gamma closer to expiry is higher)
Selling/Buying vega: selling/buying long-dated options. (Vega closer to expiry is lower)
Buying/Going long a skew: Buying low strike and selling high strike options.
Variance Swaps
A variance swap is a forwar contract on realized variance. A Long var swap payoff = notional * (realized vol2 - strike vol2)









